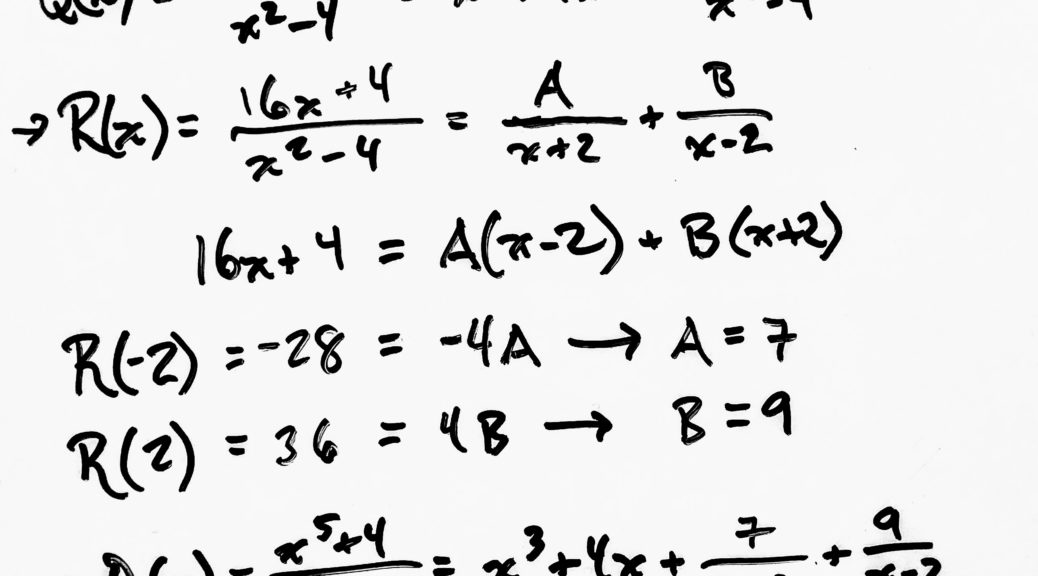
Partial Decomposition of Fractions (Easy)
Let’s be frank, practically no one in their right mind would seem to like fractions. Ever since early grade school, we’ve learned to loathe them and despise all that they stand for, right?
Honestly, I think fractions actually just get really bad rap, and it has a lot to do with the way that they’re taught.
Regardless of how you actually feel about them, whether you aren’t entirely comfortable with them or find them intimidating, you’re probably going to find partial decomposition of polynomial fractions to be downright nightmarish.
Here at MathSamurai, though, it’s all about turning those ugly boogeyman monsters into at least manageable pests (if not downright entertaining problem-solving puzzles). So let’s take a deeper look at what this horrendously named yet simple concept is really all about.
Let’s start with a fairly simple problem,
$$\frac{x^5+4}{x^2-4}$$
The first thing we need to check for here, before splitting up anything by its denominators, is whether we’re looking at an improper fraction or not. In layman’s terms, let’s check to see if the polynomial up top (the numerator) is bigger or smaller than the one below (the denominator).
In grade school, if you were looking at something like \(\frac{5}{2}\), you were often expected to rewrite that as a mixed fraction. (At some point down the road you stopped having to do that so often, but that skills ends up being really important for the more complicated-looking polynomial division we’re about to do.) To get that mixed fraction, you had to actually divide 2 into 5, then write some remainder next to it, designating it the remainder by writing “R” next to it.
$$\quad{2\;R\,1}\\
{2\;)\overline{\;5\qquad}}$$
So we’ll have to perform a little polynomial long division for this one. That’s just a fancy way of saying, let’s see how many times \(x^2-4\) goes into \(x^5+4\):
$$x^2-4\;)\overline{\;x^5+4}$$
Just as I’ve written elsewhere, for polynomial division you don’t write “R” for the remainder anymore, but you do actually use the same process for dividing. So notice that we could write \(\frac{5}{2}\) with its remainder as either \(2\;R\,1\) or \(2+\frac{1}{2}\). Notice of course that’s just another way of saying “two and a half” (and, in case you were wondering, has exactly the same meaning as writing \(2.5\), since \(\frac{1}{2}=.5\;\rightarrow\;2+\frac{1}{2}=2.5\) ).
So when we divide the denominator in the numerator, we now get,
$$x^3+4x+\frac{16x + 4}{x^2-4}$$
Now we can just turn our attention to the proper fraction, that is the part on the far right with its numerator smaller than the denominator, and leave the rest of the polynomial behind until the very end.
Let’s just take \(\frac{16x+4}{x^2-4}\) and think about what it’ll have to be equal to. We’re going to stick in some variables for our use to figure out the numerator, but first let’s think about what the denominator is going to look like.
If we’ve been doing a lot of factoring of quadratic expressions [quadratic factoring link] recently, it might dawn on us that this looks exactly like a difference of squares. (That’s because it is!)
So we can rewrite \(x^2-4\) as \((x+2)(x – 2)\). Since those are the two factors that would make up the denominator of the big fraction when combined, that means they are each going to become their own denominator in the bottom of the “smaller” fractions we’re breaking them up into:
$$\frac{16x+4}{x^2-4}=\frac{}{x+2}+\frac{}{x-2}$$
Problem solved!
Um, not quite. We still haven’t figured out the numerators yet…
So, let’s stick in those variables we talked about. The first one I’ll just call \(A\) since I still have no real idea yet what it looks like. The other one I’ll call \(B\).
$$\frac{16x+4}{x^2-4}=\frac{\color{red}{A}}{x+2}+\frac{\color{red}{B}}{x-2}$$
Now comes the part where you should start to feel relieved, because we’re going to take the nasty fractions and turn them into just a regular looking equation where we can use some fancy-shmancy algebra to solve. Let’s multiply both sides by \(x^2-4\), and notice that we get:
$$\require{enclose}\enclose{updiagonalstrike}{x^2-4}*\frac{16x+4}{\enclose{updiagonalstrike}{x^2-4}}=\Biggl(\frac{A}{x+2}+\frac{B}{x-2}\Biggr)*x^2-4\\
16x+4=\Biggl(\frac{A}{x+2}+\frac{B}{x-2}\Biggr)*(x+2)(x-2)\\
16x+4=\frac{A}{\enclose{updiagonalstrike}{x+2}}*\enclose{updiagonalstrike}{(x+2)}(x-2)+\frac{B}{\enclose{downdiagonalstrike}{x-2}}*(x+2)\enclose{downdiagonalstrike}{(x-2)}$$
$$16x+4=A(x – 2) + B (x + 2)$$
Doesn’t that look better already?
Of course, you may recognize an inherent problem to this. When you were learning systems of equations way back in Algebra 1 and 2, you probably recall that you can’t usually solve for two variables with just one equation. That is, we normally want as many equations as variables in order to solve for them.
But what if I were to set this whole thing up as a function? What that’s going to allow me to do is plug in a couple of convenient values that I can then use to derive \(A\) and \(B\).
$$f(x)=16x+4=A(x – 2) + B (x + 2)$$
Specifically, if I plug in values that make either \(A\) or \(B\) cancel entirely, we can solve for each of them separately, and that’ll solve our two-variables-one-equation issue! (Doesn’t this feel oddly reminiscent of solving systems of equations?)
So for starters, let’s plug in \(-2\) since that will cancel out \(B\) with zero.
$$f(\color{red}{-2})=16(\color{red}{-2})+4=A((\color{red}{-2})-2)+B((\color{red}{-2})+2)\\
f(-2)=-32+4=A(-4) + B (0)\\
f(-2)=-28=-4A$$
$$A=7$$
Simplifying both sides, \(A=7\). That already gives us one of our fractions! Stick in \(2\) for \(x\) and you’ll then get \(B\) since \(8\) cancels out.
$$f(\color{red}{2})=16(\color{red}{2})+4=A((\color{red}{2})-2)+B((\color{red}{2})+2)\\
f(2)=32+4=A(0) + B (4)\\
f(2)=36=4B$$
$$B=9$$
Easy peasy. Let’s take our original longer polynomial and stick \(7\) in for \(A\) and \(9\) in for \(B\):
$$\frac{16x+4}{x^2-4}=\frac{\color{red}{7}}{x+2}+\frac{\color{red}{9}}{x-2}$$
We did it!
Now, a couple of important things to keep in mind. One is that we don’t want to forget about the longer polynomial from earlier (after we converted it to a proper fraction): we should really finish solving the problem that we were given at the start.
$$x^3+4x+\frac{16x + 4}{x^2-4}\;=\; x^3+4x+\color{red}{\frac{7}{x+2}+\frac{9}{x-2}}$$
Also, it sometimes isn’t as straightforward as this example was. For instance, A and B could have turned out to be small fractions themselves (such as “\(\frac{1}{2}\)” or “\(\frac{99}{7}\)“).
But the good news is that cases like this are not really any harder than remembering that, for example, \(\frac{A}{x+2}\) is exactly the same thing as \(A*\frac{1}{x+2}\). That means that if \(A\) were a fraction, the solution would just be a matter of multiplying two fractions. Let’s assume \(A\) turned out to equal \(\frac{7}{8}\):
$$\frac{A}{x+2}\\
A*\frac{1}{x+2}\\
\biggl(\color{red}{\frac{7}{8}}\biggr)*\frac{1}{x+2}$$
$$\frac{7}{8(x+2)}$$
There are also cases where we have denominators that are far more complicated than these were. As such, we would have had to completely factor them and be sure to include a fraction with not only every factor we found but every linear combination of that factor as well. An example of both this (and the next concept below) will be demonstrated in another article.
Lastly, there’s the case where solving is slightly more complicated than simply substituting values for \(A\) and \(B\). We may be forced to restructure the polynomial using our artificial variables in creating a bunch of linear equations. In such a case, being able to solve systems of equations using matrices will definitely come in handy.
For now though, I hope we’ve managed to take out some of the fear in fractions through this example. Never forget: every samurai knows there are multiple ways to solve a problem. What are some other ways you can think of to get the same answer? Let us know in the comments below!
