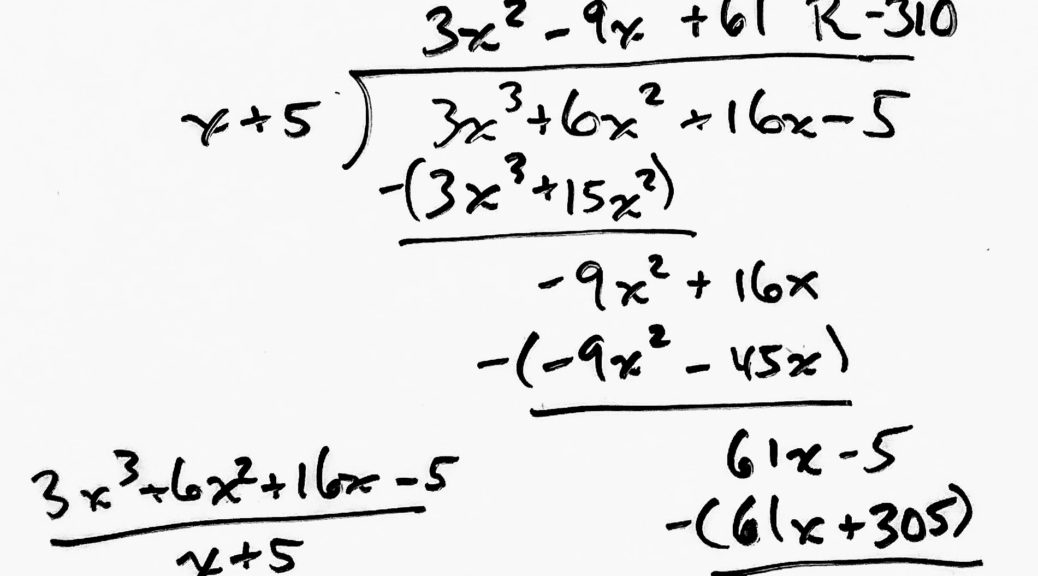
Long Division of Polynomials
So you want to divide a polynomial? Let’s say we start with a simple one like this one…
$$\frac{3x^3+6x^2 + 16x – 5}{x + 5}$$
Just kidding! I mean, we are going to do this one, but it’s hardly something you might call “simple.” That’s okay. Here at MathSamurai, we like challenges! (How else will you find out how badass you actually are?)
There are two ways to do polynomial division: the long way and the “short” way, i.e. what most people would call synthetic division. We’ll get into the synthetic stuff elsewhere, but for this post let’s cover the basics of long division (since the other has its limitations).
What if I promise you now that the procedure for long division of polynomials is as simple as the kind of long division we used to do back in elementary school? Sure, there are a couple more letters and exponents in it than you may be used to looking at, but should that really stop us?
This is a great opportunity to brush up on one of our most important “sword skills” by coming up with a simpler version of the problem we’re stuck on. And in this case, I mean really simple.
(If you’ve already done some of the fraction skill-building from other parts of this site, you can just skip right along over this section.)
Let’s take a fraction like this one then:
$$\frac{37}{2}$$
Shouldn’t be too hard for us to handle, right?
Now, back in grade school, you could get slapped across the hands with a yardstick if you didn’t simplify an improper fraction like this one. (Oh, Ms. Stacey…the trauma…) You hopefully recall that an improper fraction is just a fraction that has a bigger number in the top than in the bottom. We were always expected to take something like that and turn it into a mixed fraction that included a whole number and an (equally odd-named) proper fraction, with the top number smaller than the bottom.
But grade school is over, right? Our high school teacher actually likes improper fractions now (can’t anyone make up their mind on this matter?!), so who cares about converting them that way anymore? Besides, we know we can just stick it in a calculator and find it to be \(18.5\). So what’s the point?
The calculator method may have gotten you through the rest of elementary and middle school, but you’re entering the big leagues now. From this point forward, we’ll want to give some careful attention to the concept of mixed fractions again.
But don’t worry, you really do already understand them better than you probably think. For what is \(18.5\) but another way of saying \(18\) and \(\frac{1}{2}\), or \(18 + \frac{1}{2}\)?
That extra half is of course the remainder. It’s a result of trying to divide \(2\) into \(37\). Together, a mixed fraction like this basically says that for \(\frac{37}{2}\) of something, you’ll get eighteen chunks plus another chunk that’s half the size of all the others.
You won’t have to think about remainders this way in every case of polynomial division, but there are going to be a lot of cases where we’ll have to figure out what to do with what’s left over. So it’s a good idea to get used to it again now after not using it for so long.
Now let’s take a look at that polynomial again.
Let’s rewrite this thing long division-style, the same way you would have written \({37}÷{2}\) towards the very beginning of your math career, with the overhead line and everything:
$$\frac{37}{2}\quad\rightarrow\;37÷2$$
$$\;\\
{2\;)\overline{\;3\;7\quad}}$$
$$\frac{3x^3+6x^2 + 16x – 5}{x + 5}\\
\rightarrow\;(3x^3+6x^2 + 16x – 5)÷(x + 5)$$
$$x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}$$
There’s our setup!
So what question did you have to ask yourself back in the day in order to divide \(37\) by \(2\)? You had to get it into your head that the question was really “what is the most number of times \(2\) goes into \(3\) and then into \(7\)?” The answer for the case of \(3\) is obviously \(1\) time.
So for the harder problem, let’s try the same thing. How many times does \(x\) go into \(3x^3\)? In other words, what times \(x\) would make it \(3x^3\)? Clearly, it would be \(3x^2\). So let’s write that.
$$\quad\;1…\\
{2\;)\overline{\;3\;7\quad}}$$
$$3x^2+…\quad\quad\quad\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}$$
Back to the simpler one. We have to do something with what’s left over from \(2\) going into \(3\) one time. So we multiply \(2×1\) and put the result (\(2\)) underneath the \(3\) from our initial setup. That prompts us to subtract \(2\) from \(3\) in order to figure how much is left over for this first round of dividing.
Guess what? We’re going to do the same thing in the harder problem. So what does \(3x^2×x\) equal? Well, \(3x^3\), of course!
$$\quad\;1…\\
{2\;)\overline{\;3\;7\quad}}\\
\underline{2\;}$$
$$3x^2+…\quad\quad\quad\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}\\
\;\underline{\;3x^3\quad}\qquad\qquad\quad$$
So its divided evenly into it at this stage. Isn’t this easy so far?
Well, not quite. We actually didn’t multiply by the whole binomial \(x+5\), just the \(x\) part of it. What we should really have asked then is, what is \(3x^2\) times \(x+5\). So let’s finish fleshing that out:
$$\quad\;1…\\
{2\;)\overline{\;3\;7\quad}}\\
\underline{2\;}$$
$$3x^2+…\quad\quad\quad\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}\\
\;\underline{\;3x^3+15x^2\quad}\quad\quad$$
Next? Subtract! Note, though, that when we subtract the binomial \(3x^3+15x^2\), we’re actually subtracting both the \(3x^3\) and the \(15x^2\) from the terms above them. (Think of it as distributing the negative to each before adding them to the terms above, if that helps.)
$$\quad\quad\;1…\\
\quad{2\;)\overline{\;3\;7\quad}}\\
\;\underline{-2\;}\\
\;\quad1\;$$
$$\require{enclose}3x^2+…\quad\quad\quad\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}\\
\;-\enclose{downdiagonalstrike}{(3x^3+15x^2)}\quad\quad\quad\\
\underline{-3x^3-15x^2\quad}\quad\quad\\
\;\;0x^3-9x^2\quad\quad\quad$$
Now, what is it that you do with that \(1\) from \(3 – 2\) in our simple fraction? You bring down anything that’s left to the right of \(3\), in this case \(7\). That gives us 17.
So guess what we’re going to do for the harder problem? It’ll be just a little bit trickier because we may actually be missing a place, perhaps where there is actually a 0x or simply nothing of that term. As long as we’re really careful with it, we can bring down things just the same way though.
$$\quad\quad\;1…\\
\quad{2\;)\overline{\;3\;7\quad}}\\
\quad\underline{-2\;}\downarrow\\
\;\quad1\;7$$
$$3x^2+…\quad\quad\quad\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}\\
\underline{-3x^3-15x^2\quad}\downarrow\quad\\
\quad\quad\quad-9x^2+16x\;$$
That’s it, rinse and repeat! The hardest part is just paying close attention to detail and not missing anything along the way. Here’s what it looks like when we’ve gone as we can go for both fractions.
$$\quad\quad\quad1\;8\;R\,1\\
\quad{2\;)\overline{\;3\;7\quad}}\\
\quad\underline{-2\;}\quad\\
\;\quad1\;7\\
\quad\quad\underline{-1\;6\;}\quad\\
\;\quad\quad\quad1\quad\\$$
$$\qquad3x^2-9x+61\;R\, ¯310\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}\\
\underline{-3x^3-15x^2\quad}\quad\quad\\
\quad\quad\quad¯9x^2+16x\;\\
\;\qquad-\enclose{downdiagonalstrike}{(¯9x^2-45x)}\quad\\
\qquad\quad\quad\underline{9x^2+45x\quad}\\
\quad\qquad\qquad\qquad61x-5\\
\qquad\qquad\qquad\qquad-\enclose{downdiagonalstrike}{(61x+305)}\quad\\\
\,\qquad\qquad\qquad\qquad\underline{¯61x-305\quad}\\
\;\qquad\qquad\qquad\qquad\qquad¯310\;$$
So everything was going just fine, but now we have that \(¯310\) just sticking out there on the end. What do we do with it?
Remember how remainders of simple fractions are the same thing as just the whole number plus whatever is remaining over the divisor (the official name of the number you’re dividing by)? The same concept applies here to both the simple case and the polynomial case. We can rewrite these as,
$$\quad\quad\quad1\;8\;R\,1\\
\quad{2\;)\overline{\;3\;7\quad}}$$
$$\rightarrow18+\frac{1}{2}$$
$$\qquad3x^2-9x+61\;R\, ¯310\\
x+5\;)\overline{\;3x^3+6x^2+16x-5\quad}$$
$$\rightarrow3x^2-9x+61-\frac{310}{x+5}$$
So hopefully it’s clear now how simple long division really is, whether you’re working with your everyday elementary school natural numbers-type fractions or your more intimidating-looking polynomial ones. After doing a few of these, you’re bound to find these fairly easy to solve, but you’ll probably start wondering as your writing hand begins to ache: “Is this really the shortest way through these woods?”
The answer as usual is no. Next time, we’ll take a look at synthetic division and how it can be a bit of a time saver (as long as you’re sticking with binomial divisors like \(x+5\) and not crazier ones such as \(8x^2+28x-2\)). Regardless, this simple, however time-consuming, technique will get you a long way through simplifying polynomial expressions (sometimes just called rational expressions) or cutting polynomials down to size a bit for the sake of factoring and finding zeroes for an equation.
Never forget: every samurai knows there are multiple ways to solve a problem. What are some other ways you can think of to get the same answer? Let us know in the comments below!
